-
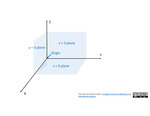
Infinitesimal Elements in Cartesian, Cylindrical and Spherical Coordinate Systems
Ashanthi Maxworth PhD
In this chapter we introduce you to the infinitesimal surface and volument elements in Cartesian, Cylindrical and Spherical coordinate systems. Electromagnetic fields is based on multi-variate vector calculus. The following three documents show, how the infinitesimal surface area elements are defined in Catesian, Cylindrical and Spherical coordinate systems.
-

Maxwell's First Equation: the Gauss's Law for Electrostatic Fields
Ashanthi Maxworth PhD
Gauss's Law for electrostatic fields states the net electric flux through a closed surface is proportional to the total charge enclosed. Under the assumption that one charge produces only one flux, the Gauss's Law states that the net electric flux through a closed surface is equal to the total charge enclosed. The applications of Gauss's Law includes, electro-filters, xerographic printing, electrostatic sheilding and many more. Watch the two short videos where Dr. Maxworth explains the Gauss's Law for electrostatic fields and derive the capacitance of a parallel plate capacitor. Then you may complete the Ansys worksheets on the parallel plate capacitor. In the third video she explains the derivation of the capacitance of a coaxial cable. Make sure to watch that video and you may complete the Ansys worksheet on the electric field inside a coaxial cable.
-

Maxwell's Second Equation: the Gauss's Law for Magnetostatic Fields
Ashanthi Maxworth PhD
Gauss's Law for magnetostatic fields says that the total magnetic flux through a closed surface is equal to zero. In otherwords, there are no magnetic monopoles. This law has been applied in multiple mathematical derivations. Watch the short video where Dr. Maxworth explains this law. In the worksheet you can observe the magnetic flux generated due to a current through a straight coaxial cable. Note that the magnetic flux always exisit as close loops making the total net flux through a closed surface zero and the direction of the magnetic field can be derived by the right hand rule, i.e when you point the thumb of the right hand the direction of curling fingers indicate the direction of the magnetic field.
-

Maxwell's Third Equation: the Faraday's Law
Ashanthi Maxworth PhD
Faraday's Law states that the voltage induced in a closed loop is equal to the rate of change of magnetic flux through that loop. As we know, when there is no fluctuating magnetic flux, there is no voltage difference across a closed loop. But when there is a changing magnetic field, a voltage is induced within a closed loop known as the electromotive force or the EMF. There are two types of electromotive forces: the motional EMF and the transformer EMF. In motional EMF the magnetic field is kept steady while the loop is moved such that it cuts the magnetic field varying the total magnetic flux through the coil, similar to a dynamo. In transformer EMF, the loop or the coil is kept stationary while an alternating current is run through the coils to generating a time-varying magnetic field. The Faraday's Law has the most number of applications out of all Maxwell's Equations. The applications of the Faraday's Law include, induction cooking, wireless power transfer, metal detectors, electromagnetic breaks and all forms of eddy current applications. The eddy currents are current loops formed on metalic surfaces when exposed to a time-varying magnetic field. In the following video Dr. Maxworth explains the Faraday's Law and and the point form of Maxwell's equations. Then you may proceed to the worksheets on mutually coupled transmission lines and wireless power transfer.
-

Maxwell's Fourth Equation: the Ampere's Law
Ashanthi Maxworth PhD
The original Ampere's Law indicated the total magnetic field intensity along a closed loop is equal to the current enclosed. It was Dr. James Clerk Maxwell who introduced the missing term which was the rate of change of electric flux which is also known as the displacement current. As shown in the video of Faraday's Law and the Point form of Maxwell's Equations, the full Ampere's Law says the total magnetic flux along a losed loop is equal to the conduction and displacement currents. In this video Dr. Maxworth uses the original Ampere's Law to derive the inductance of a coaxial cable. The displacement current introduced by Maxwell, showed that a time varying electric field can create a time-varying magnetic field. Combining all of these four equations, comes the electromangetic fields, where a time-varying electric field creates a time-varying magnetic field, and in-turn a time-varying magnetic field creates a time-varying electric field, overall creating a propagating electromagnetic field. In the worksheet, you can observe different modes of a propagating electromagnetic fields inside a rectangular waveguide.
Printing is not supported at the primary Gallery Thumbnail page. Please first navigate to a specific Image before printing.





